How structured do PCP queries need to be?
14 Apr 2021Although lower bounds in complexity theory usually refer to impossibility results related to how time or space efficient an algorithm for a class of problems can be, I do think that this question, about the entropy of queries of a PCP, is a sort of lower bound on how oblivious or lazy a verifier can be. Entropy and information gain are important and old concepts in machine learning, but I think that in the age of deep learning, people don’t realize just how wide the concept of a learning algorithm can be stretched. Fields like cryptography often focus on transmitting some very specific, structured knowledge and hide everything else, which is a nice dual perspective to machine learning. Verifiers and extractors are learners, too. Unsurprisingly, techniques from cryptography can show up in machine learning. Alex Irpan has a cool blog post showing how the hybrid argument (which shows up in my proof of the not-uniform-but-still-independent case) appears in imitation learning (RL) proofs.
 source: xkcd.com
source: xkcd.com
Just as the Turing Machine provides an abstract lens through which we can study computation in general, interactive proofs provide a template through which theorists can characterize specific classes of computational problems. In the most basic form, interactive proofs can be thought of as a game between two parties, a prover and a verifier. The prover and verifier are each Turing machines which perform their own computations. The interactive proof model allows the two parties to communicate, and the behavior of one may alter the behavior of the other.
Often times, the kinds of protocols that people design interactive proofs are for proofs of membership. That is, the prover knows that some string \(x\) belongs to some set \(L\) and wants to convince the verifier to believe that this is so, i.e. that the statement “\(x\) belongs to the language \(L\)” is true. In general, this set \(L\) can be almost anything - it can be the set of graphs that are 3-colorable, the set of descriptions of Turing Machines which halt when run on their own description, or (for the sake of imagination) the set of true mathematical statements.
Formally, a language \(L\) in computer science is defined with respect to an alphabet, Σ, which is a (usually finite) set of symbols. A language \(L\) is simply a subset of the possible strings that can be formed using the symbols in \(\Sigma\).
As anyone who has taken a proof-based math class can tell you, verifying a chain of arguments purportedly convincing you of the veracity of statement is an arduous task. There are so many things that could go wrong–a mishap of calculation, a faulty act of modus ponens, starting from wrong assumptions–among others. If there is a mistake, you must catch any instance of such a mistake, but you do not know a priori what the mistake will be or where in the proof it will occur. In this view, the verifier must carefully read, line by line, a proof, “remembering” what it has seen before, in order to catch an inconsistency.
If P is the class of languages that can be solved efficiently (the set of languages for which membership can be decided efficiently), then class NP is exactly those languages which have proofs of membership which can be verified efficiently.
The class NP is often defined with respect to the notion of a witness. A language \(L\) is said to be in NP if for every string \(x \in L\), there exists another string \(w\), not much longer than \(x\), that bears witness to this fact. And for every \(x \not \in L\), no such string (longer than x by a polynomial factor), can convince the NP verifier otherwise.
The non-interactive proof protocol for an NP goes as follows. The prover and verifier are each given \(x\) as inputs, but the prover additionally is given the witness for \(x\), \(w\). The prover sends w directly to the verifier. The verifier checks \(w\) to decide whether \(x \in L\), typically in the process reading the entire proof, \(w\).
The existence of a type of proof called a probabilistically checkable proof (PCP) tells us that, actually, there are certain (interesting!) languages which have proofs that can be checked by reading just a few spots in the proof. For certain problems, including graph 3-colorability, membership can be verified in a “lazy” way. That is, given a NP language \(L\) and a statement \(x\), I have a generic way of reading just three bits of any alleged proof and decide with high confidence whether \(x \in L\).
Instead of thinking about the interaction between a prover and a verifier, we focus primarily on a verifier, who now has oracle access to a proof string π. The verifier has arbitrary access to a string which encodes the proof \(\pi\) that some \(x\) belongs to the language \(L\). On input \(x\), the verifier tosses some \(r(n)\) coins to decide some \(q(n)\) indices to read the proof at. In the course of its execution, the verifier is allowed to do arbitrary computations as long as its running time is bounded by \(t(n)\). At the end, the verifier outputs a single bit deciding the status of \(x\).
 from Eli Ben-Sasson’s notes
from Eli Ben-Sasson’s notes
The PCP Theorem proved by Arora, Lund, Motwani, Sudan and Szegedy says that NP = PCP(length = \(poly(n)\), randomness = \(O(log(n))\), query = \(O(1)\), time = \(poly(n)\)). That is, the class of efficiently verifiable languages is exactly those which have PCPs where the proof string is only polynomially longer than the input length, the (efficient) verifier flips only logarithmically many coins, and asks to read the proof at only a constant number of bits.
The particular instantiation of the PCP template used to prove the ‘basic PCP Theorem’ involved using error correcting codes to encode the NP witness \(w\). Error correcting codes, originally designed for communicating over faulty channels, have the property of redundancy. This in turn amplifies any errors that occur in the original proof, \(w\), making inconsistencies easier for the verifier to catch.
At this point, my intuition started twitching. It seemed weird that regardless of the input or witness size, you could read a fixed number of bits of a proof and be convinced of the veracity of a statement. It was basically saying that for NP, the languages which can be efficiently verified, verification only depends on a small, fixed number of junction points.
Which lead me to ask, how much knowledge does the verifier need to have of where to look? How simple can the verifier be? Can it haphazardly make any set of random queries? In particular, if the number of queries is k, can the verifier make k k-wise independent uniformly random queries?
It seems that all known PCP constructions use correlated queries in the verifier to achieve the soundness requirement (so that the verifier can catch a cheating prover trying to claim some x ∉ L is otherwise.)
For example, the Hadamard PCP uses three queries \(x, y, z\). The first two are uniformly and independently chosen, but the third is \(z = x+y\). But what specifically happens if we let x,y,z be 3-wise independent? It turns out that you get results that are in contradiction with certain strongly believed conjectures in computer science, in particular we get that co-RP = NP.
In complexity theory, folks are concerned with classifying the inherent difficulty of computational problems on fundamental measures like time and space. There’s an entire hierarchy of more and more difficult problems, and many practical things depend on the separation of classes within this hierarchy. For example, the security of public key cryptography (i.e. the infrastructure of the internet) depends on P \(\ne\) NP. co-RP \(\ne\) NP is a similar, albeit less dramatic, such statement, and is conjectured to hold. Every time someone writes a paper stating otherwise, people get pretty excited. Because these conjectures are widely accepted, people can prove statements in complexity theory by showing that the contradiction would invalidate one of the conjectures. co-RP \(\ne\) NP is implied by a conjecture called the exponential time hypothesis.
If the PCP verifier can get away with uniformly random k-wise independent queries to the proof string, then we are basically saying that what matters is the relative frequency of symbols in the string and not their order. Restricting our attention to bit strings, all the PCP verifier needs to know in order to decide whether \(x \in L\) is a histogram of the number of 0s and the number of 1s in the string. We can use this observation to construct an co-RP machine to decide an arbitrary NP language, thus proving co-RP = NP (as co-RP is already known to be contained in NP.)
We essentially go about the business of guessing what the correct distribution of 0s and 1s should be for a valid proof string \(\pi\) of \(x \in L\). Since \(\pi\) is only polynomial in length, and we are dealing with bit strings, then there are only polynomially many possible histograms, and we can try them all with only a polynomial overhead in running time. (To see that there are only polynomially many histograms, note that the histogram is completely determined by the number of 0’s present in a proof string. If your proof string is of length N, then the number of 0’s can have is between 0 and N, giving N+1 histograms.)
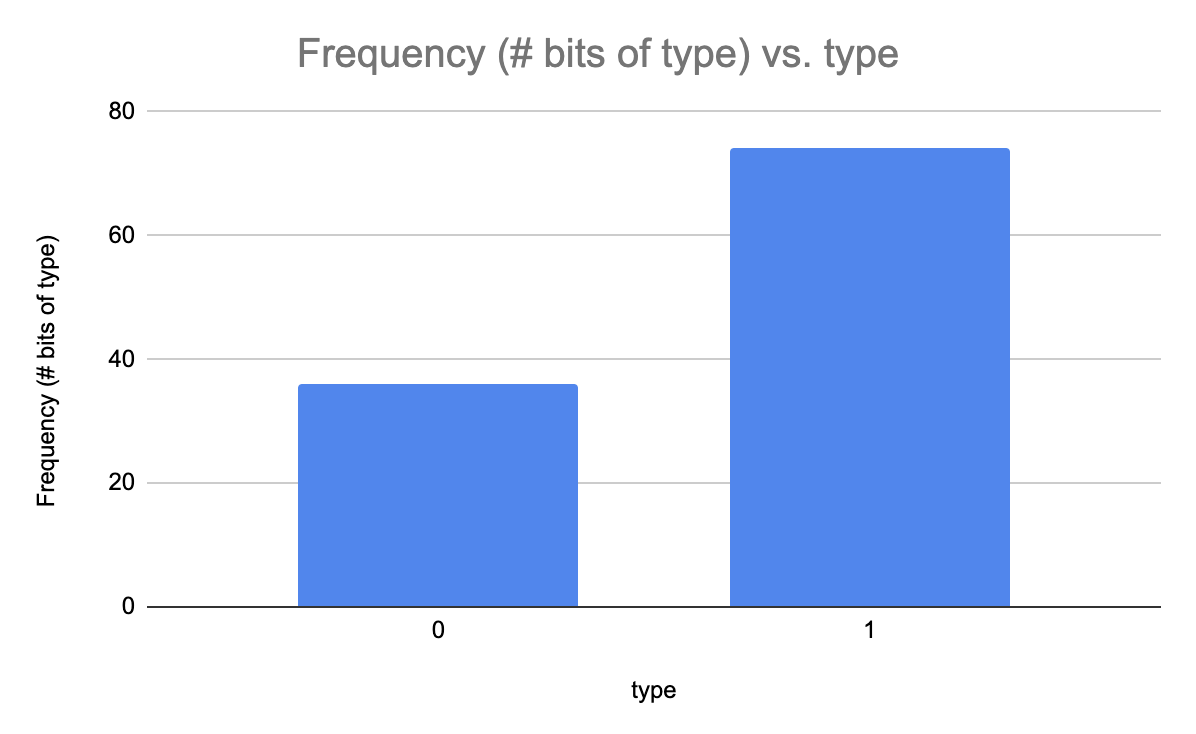
For a language L ∈ NP, we construct an RP machine M that decides L. Since NP = PCP(poly(n), log(n), O(1)), there is a PCP verifier V that reads polynomial length proofs and makes a constant number, k, of queries to the proof oracle. Our machine M will act as the proof oracle and answer any oracle queries V makes. On input x, M will iterate through every possible histogram for the proof π. M will run V on this proof, meaning M will run V, and every time V makes a proof query, M will simulate the answer by flipping a biased coin that has the exact bias as dictated by the histogram of π. If for any histogram, V accepts, then M accepts. By completeness of the PCP protocol, if x ∈ L, then there exists a histogram on which V will accept, and thus if x ∈ L, M will accept with probability 1. On the contrary, if x ∉ L, by soundness of the PCP protocol, no matter what the histogram is, V accepts with probability less than a. Thus, for x ∉ L, the RP machine M will reject with probability at least 1 - p(n) ⋅ a.
Here, we have assumed that the alphabet we operate on is constant in size. This is important for the sparsity of possible histograms that summarize the possible proof strings for the PCP verifier, though it is possible to think about computation on polynomial-sized alphabets. When we move to polynomial-sized alphabets, we lose the property of sparsity of possible histograms that summarize all possible proof strings. If the proof string is of length N = p₁(n) and the alphabet size is k = p₂(n), then the number of possible histograms is equivalent to choosing N objects from a set of size k, with replacement–which in particular is bounded below and above exponentially,
\[\big( \dfrac{k + N - 1}{N} \big)^N \le \big( \binom{k + N - 1}{N} \big) \le \big( \dfrac{e(k+N-1)}{N} \big)^N\]In other words, if we follow the same strategy, we would incur an exponential runtime. However, we can still achieve similar complexity theoretic statements as with the constant alphabet version.
The trick is to use an approximate set cover. Basically, we summarize groups of similar proof strings by a representative proof string. Then instead of checking all possible histograms, we check only the histograms of the set of representative strings. The important part is that our set of representative strings (a) covers the original set well and (b) is polynomial in size.
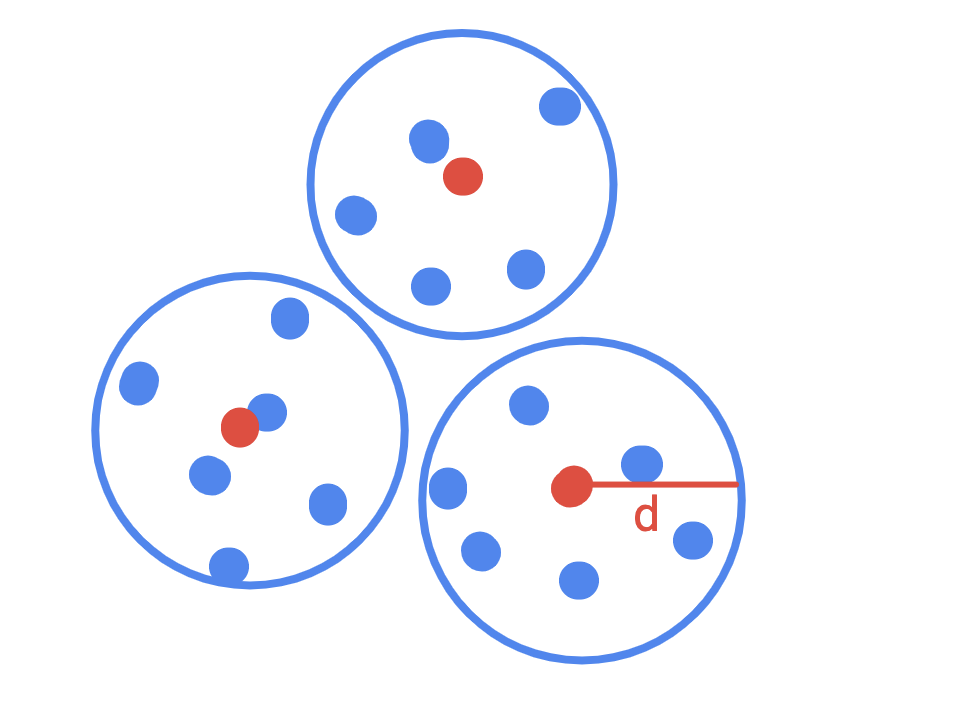
What do we mean exactly by “covers the original set well?” Our goal is to construct a polynomial-time algorithm to decide \(L\) guaranteed to accept on \(x \in L\) and with error \(\le \frac{1}{2}\) on \(x \not \in L\), so we can show the impossibility of query-efficient uniformly random query PCPs on polynomial size alphabets.
Suppose that we start with a PCP system in which the verifier accepts on \(x \not \in L\) with probability less that or equal to some constant \(0 < s \le \frac{1}{2}\). And this PCP system has some set of proof strings \(\mathcal{S}\). Then, we want to produce a set cover of the proof strings using random strings, \(\mathcal{S}'\), such that on this new set \(\mathcal{S}'\) we can verify \(x \in L\) with probability \(1\) and we will still err on \(x \not \in L\) with probability \(\le \frac{1}{2}\). If we can produce a set \(\mathcal{S}'\) of strings that are statistically close to the original set, then we can argue that our new proof system using \(\mathcal{S}'\) is sound by appealing to the soundness of the original PCP system. If the verifier accepts with high probability on the random histogram, then there exists a fixed histogram on which the verifier accepts with high probability. In complexity theory, we call this an averaging argument, though I believe it is an instance of the more generic probabilistic method.
What we care about is the distance between two distributions–the distribution that the verifier sees when sampling from a string in \(\mathcal{S}\) and the distribution that it sees when sampling from a string in \(\mathcal{S}'\). If the verifier cannot distinguish between them, then our averaging argument goes through. The cool thing is that we can define the statistical distance between two distributions relative to the verifier’s perspective!
Consider summarizing each polynomial length proof string by sampling UAR with replacement \(100k^2\) spots on it. Then when the verifier makes its \(k\) uniformly random samples, as long as the verifier does not sample twice the intermediate \(100k^2\)-length string, the new sampling strategy replicates sampling UAR from the original proof string. This formulation allows us to bound the statistical distance between the two distributions by the birthday paradox. (Consider thinking about it like this: sampling the string \(100k^2\) times UAR is like running the original verifier \(100k\) times with fresh randomness each time… We then forget about all but \(1\) of those runs.)
Let \(R(X)\) be a random variable denoting \(V\)’s output when using the original proof strings \(\mathcal{S}\) and let \(R(Y)\) be a random variable denoting \(V\)’s output when using \(\mathcal{S}'\). Then \(\vert Pr(R(X) = 1) - Pr(R(Y) = 1) \vert < c \cdot s\) where \(0 < c < 1\) is a constant. Actually, \(c\) is the probability of collision given by the birthday paradox, which is approximately \(1 - e^{-n^2 / 2d}\) when throwing \(n\) balls into \(d\) bins. Plugging in \(k,100k^2\), we get \(c \approx 0.005\).
This is good enough to write a new co-RP algorithm for the polynomial-size alphabet case. We use repetition and the union bound to drive the soundness error down to \(< \frac{1}{2}\), and you can read about the details here as well as the extension of the original question to the case where the PCP verifier queries are no longer uniform but still independent. (It uses a weighted histogram!)
Although lower bounds in complexity theory usually refer to impossibility results related to how time or space efficient an algorithm for a class of problems can be, I do think that this question, about the entropy of queries of a PCP, is a sort of lower bound on how oblivious or lazy a verifier can be. Entropy and information gain are important and old concepts in machine learning, but I think that in the age of deep learning, people don’t realize just how wide the concept of a learning algorithm can be stretched. Fields like cryptography often focus on transmitting some very specific, structured knowledge and hide everything else, which is a nice dual perspective to machine learning. Verifiers and extractors are learners, too. Unsurprisingly, techniques from cryptography can show up in machine learning. Alex Irpan has a cool blog post showing how the hybrid argument (which shows up in my proof of the not-uniform-but-still-independent case) appears in imitation learning (RL) proofs.
I’ve also been told that my line of reasoning about PCP proofs is similar to the uniform-distribution PAC learning model, where examples \((x, f(x))\) are drawn uniformly at random, i.e. as opposed to a machine being able to make membership queries “is \(x\) an example of C”?
“General PAC-learning insists that one algorithm works simultaneously for all distributions. In fact, the machine learning community interested in real-world applications finds the uniform setting questionable: “They’ll punch you in the nose if you try to tell them about algorithms in this framework.” –Ryan. But, in a more general framework, no one can really prove anything.”
I guess I was just trying to make the problem easier so I could say something about it! XD
Acknowlegements: This work was the result of questions I had while first learning about PCPs, and I thank Justin Holmgren for coming up with the elegant answer using the birthday paradox. I also thank Fermi Ma, Orr Paradise, Alex Lombardi, and Li-Yang Tan for talking to me about proof systems. (My oracles for theoretical CS!)
